Possible paths in a nxn grid
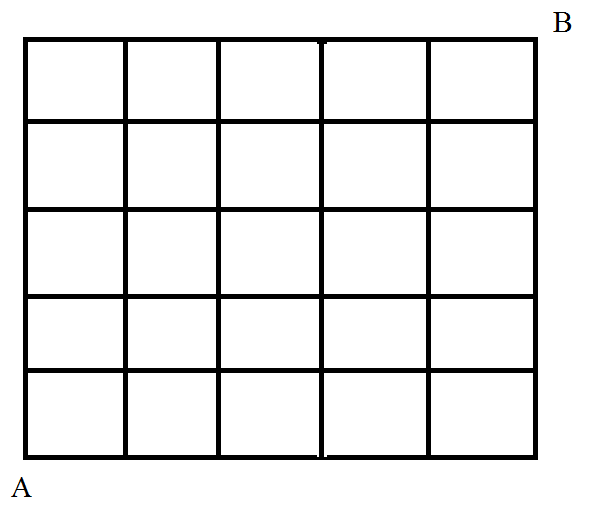
Problem Statement: You are standing on the point A in a city where roads are represented as lines and each corner is a stop. You need to get to your office and it is boring to go by the same route everyday, so the company has given you to choose from a list of cities each having a layout of n x n grid, now you have to work for a year in a city you choose, your job is to choose a city in which you can go to office having a new route everyday, just to keep things more interesting.
Solution:
We will first understand the problem using a small problem of 3 x 3 grid and see ho many possible routes possible there.
Let us represent a move up as U and a move right as R, from the figure it is clear no matter how we move, to get to point B we need exactly 3U and 3R moves, as we need to cover 3 unit distance up and 3 unit distance right and in total six steps.
It is important to note that the order of moves doesn't matter and that is the key to solve this problem, for example we can go by RRRUUU or UUURRR or URURUR, we will reach the point B in each case. Hence the problem boils down to fact that how to place 3U's in 6 position. or we can say 3R's in 6 positions.
That's simple we have to place 3 objects in 6 places, hence 6C3 possible configurations.
So we will have 6C3 = 20 combinations of routes possible.
A slightly different way of analyzing the same could be that the number of possible routes is nothing the the different number of words we can form by shuffling RRRUUU in their positions, so we have 6 different letters to shuffle hence 6!, but wait we also have R repeating three times and same for U, hence we need to divide those 3! combinations, hence we will get 6!/(3! * 3!) which is equal to 20.
Now we can solve the original problem, we know that there are 365 days in a year (Considering the non-leap years), so we need to find the dimension of the city n x n so that we can get 365 different routes for a day, from the previous example it was clear that we needed to 3 U moves and 3 R moves to go from point A to point B in case of 3 x 3 matrix, similarly here we will need n U moves and n R moves to get to point B,
So we have to shuffle n U moves and n R moves, total we have 2*n moves to arrange hence (2*n)! but n U moves are repetitive and n R moves are repetitive, hence we divide those combinations, so total no. of possible combinations here is equal to (2*n)!/(n! * n!)
which can also be said as placing n objects in 2*n slots, hence (2*n)Cn combinations.
Now the value (2*n)!/(n! * n!) must be greater than or equal to 365, we have the equation as (2n)!/(n!* n!)>=365, now to solve this we will use hit and trial, we will plug in some values of n and get the result.
For n = 5; (2n)!/(n! * n!) = 252
For n = 6; (2n)!/(n! * n!) = 924
So atleast we need 6 x 6 city layout in order to have a different route everyday in a year.
Thank you folks, hope you find the article interesting, have a nice day!