Why circumference of a circle is 2πr and area is πr^2 ?
- Saransh Dabas
- Feb 28, 2017
- 3 min read
From where did π came ? During the very early days of mathematics, people had a great use of circles, circles were everywhere, for examples in tires, motors etc. therefore they had a good knowledge of circles and they know that a perfect circle of any size has this remarkable property, the ratio between the circumference and the diameter of the circle is always the same and that constant being called as pi denoted by π. So that's where the pi came and this constant is an irrational number i.e it has no end for its decimal digits.

So, today we are going to see that how the area and circumference of a circle being equal to πr^2 and 2πr respectively, here it comes:
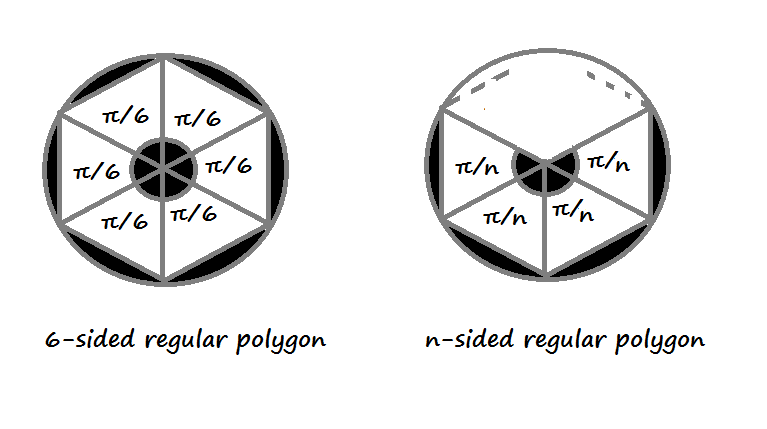
1) Proof of circumference using n sided regular polygon figure
a) Using inscribed polygon
Consider a polygon of n sides inscribed in a circle of radius r, then angle formed by the two radii at the center and one of the side of the polygon will be equal to 2π/n as from the symmetry the whole angle 2π is divided into n parts, this will be clear from the following figure :
Now, we will see what happens when the value of n becomes larger and larger, here is a rough figure:
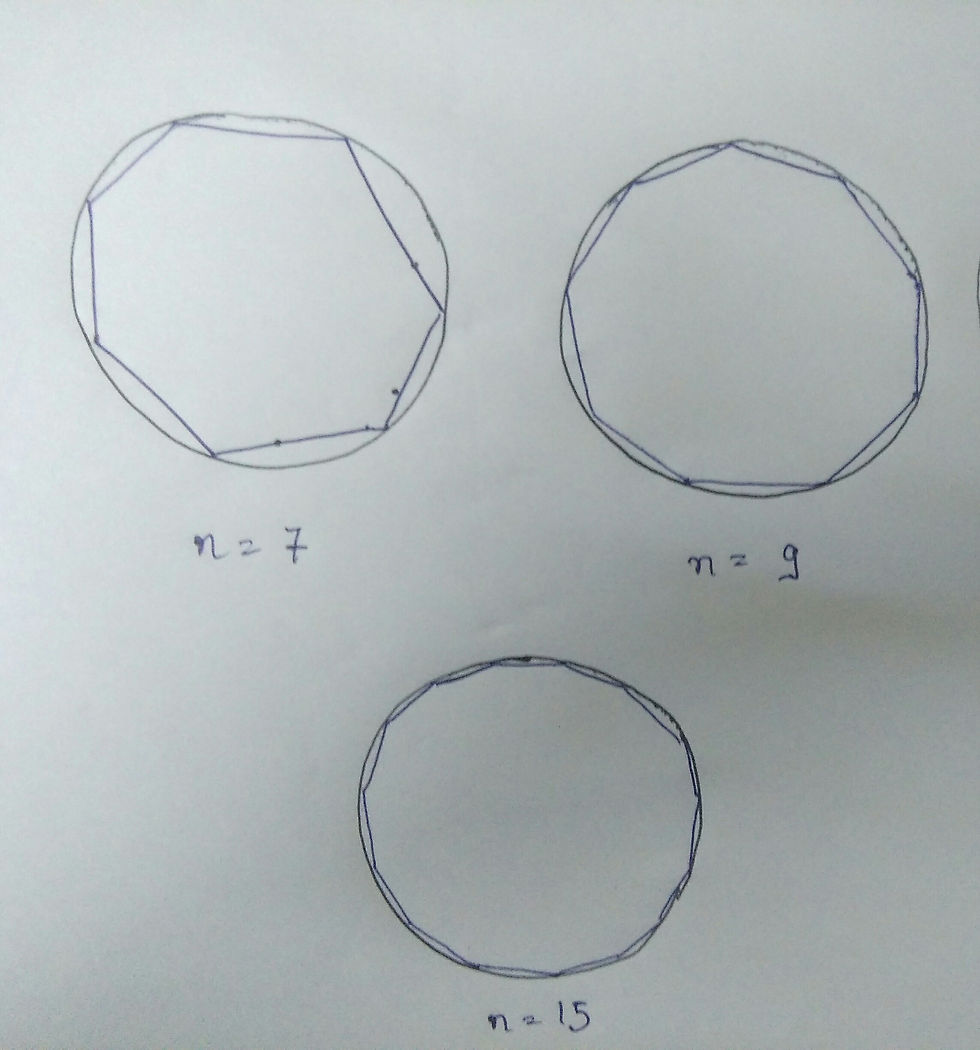
We can observe that as the value of n increases, the number of sides obviously increases but also the length of each side decreases and come closer and closer to circumference and as n tends to infinity the sides actually tends to become a point and their will be infinite points forming the circle, hence the sum of length of sides actually becomes the circumference of the circle as n tends towards infinity, by summing up these infinitely many sides we will get the circumference, to do the same we need some trigonometric and geometric concepts, as shown below:
Let us concentrate on one side and then we will sum up all of them to get the circumference, as from symmetry the sum of lengths of all sides will be equal to n times the length of a side.
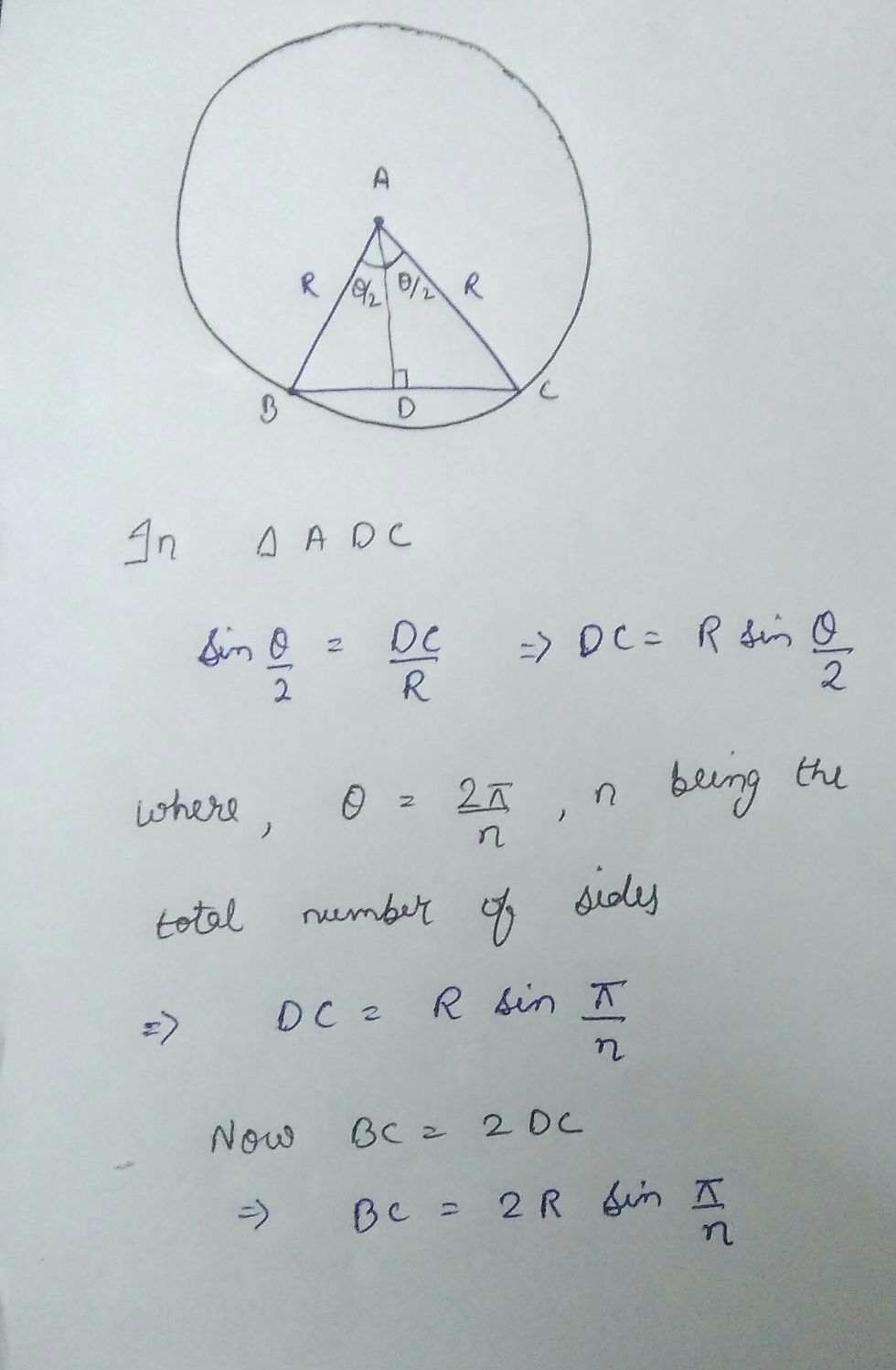



b) Using inscribed circle Let us consider a circle inscribed in an n sided polygon, same as in above case if n tends to infinity the sides of the circle will come very very close to the circumference of the circle.

So, that was one way to prove it, however their exist a much easier way which is based on integral calculus.
2) Integral calculus to find the circumference
I will discuss Integral Calculus in detail in separate category, you can find the link at the end of this article.
We consider a really thin strip of circle and let's say that it subtends really small angle dθ
at the center, Now the length of the arc will be Rdθ and we integrate this function with respect to theta where theta varies from zero to 2π.

2) (a) Integral calculus to find the area
The very fundamental definition of integral calculus says that it is the sum of the areas of infinitesimally thin strips which gives the whole area of the figure. I will discuss Integral Calculus in detail in separate category, you can find the link at the end of this article.
We consider a really thin strip of circle and let's say that it subtends really small angle dθ
at the center, Now we will calculate the are of this thin strip and integrate it over the angle of 360 or 2π.


b) Area of circle using limits:
Consider a triangle in a n sided polygon inscribed in a circle and then calculate the area of this triangle, and the area of the circle will be n times the area of triangle as n tends to infinity.
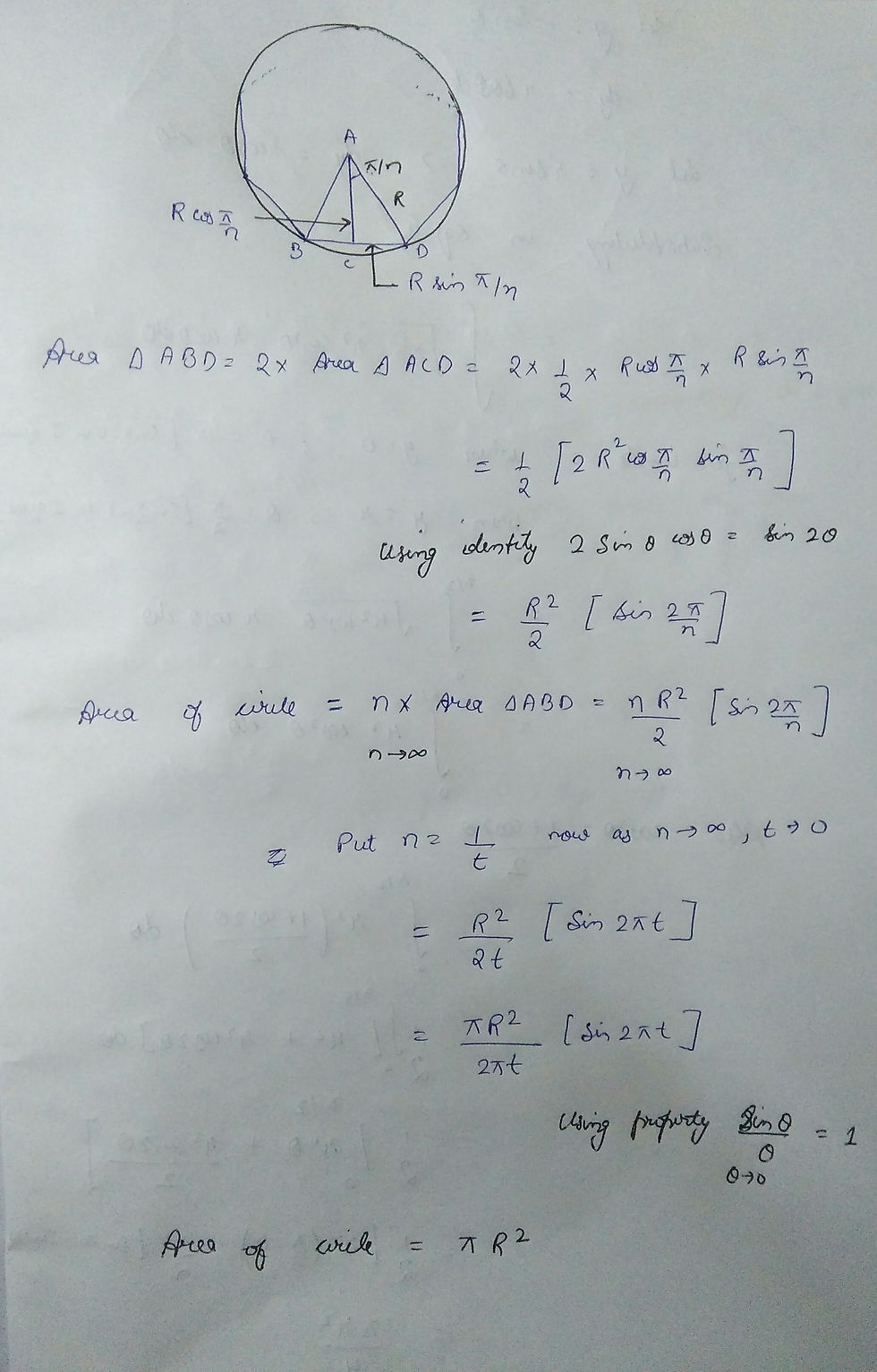
Thank's for reading folks, hope you like the article, have a nice day!
Comments