Evaluating the nested radical.

Infinite series are one of the most beautiful looking expressions in mathematics and it is fun to solve them, sometimes they converge to a finite value sometimes they do not, hence called convergent and divergent series respectively.

Today we are going to look a class of infinite series which is the nested radicals. In high school we have these kinds of problems to solve like this one.

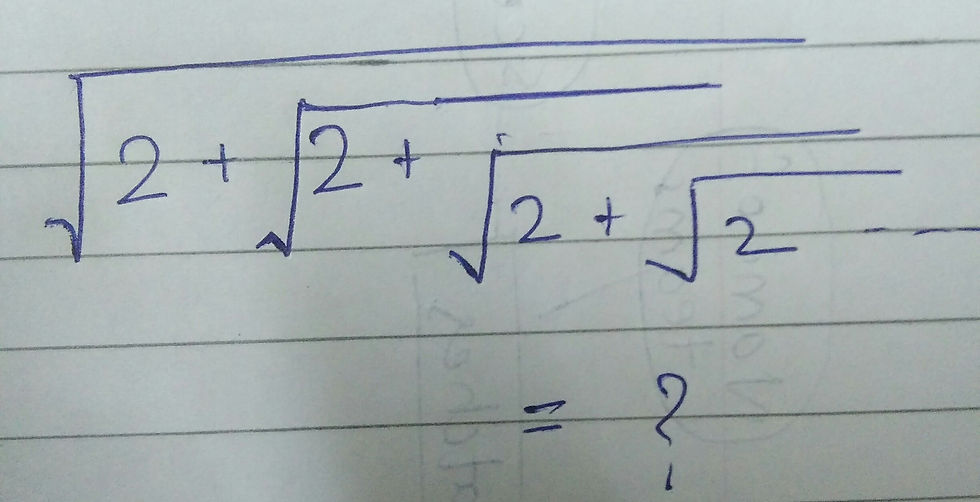
Its pretty easy to solve the above expression, we can write the function recursively and then solving the quadratic equation formed. Here is the proof :

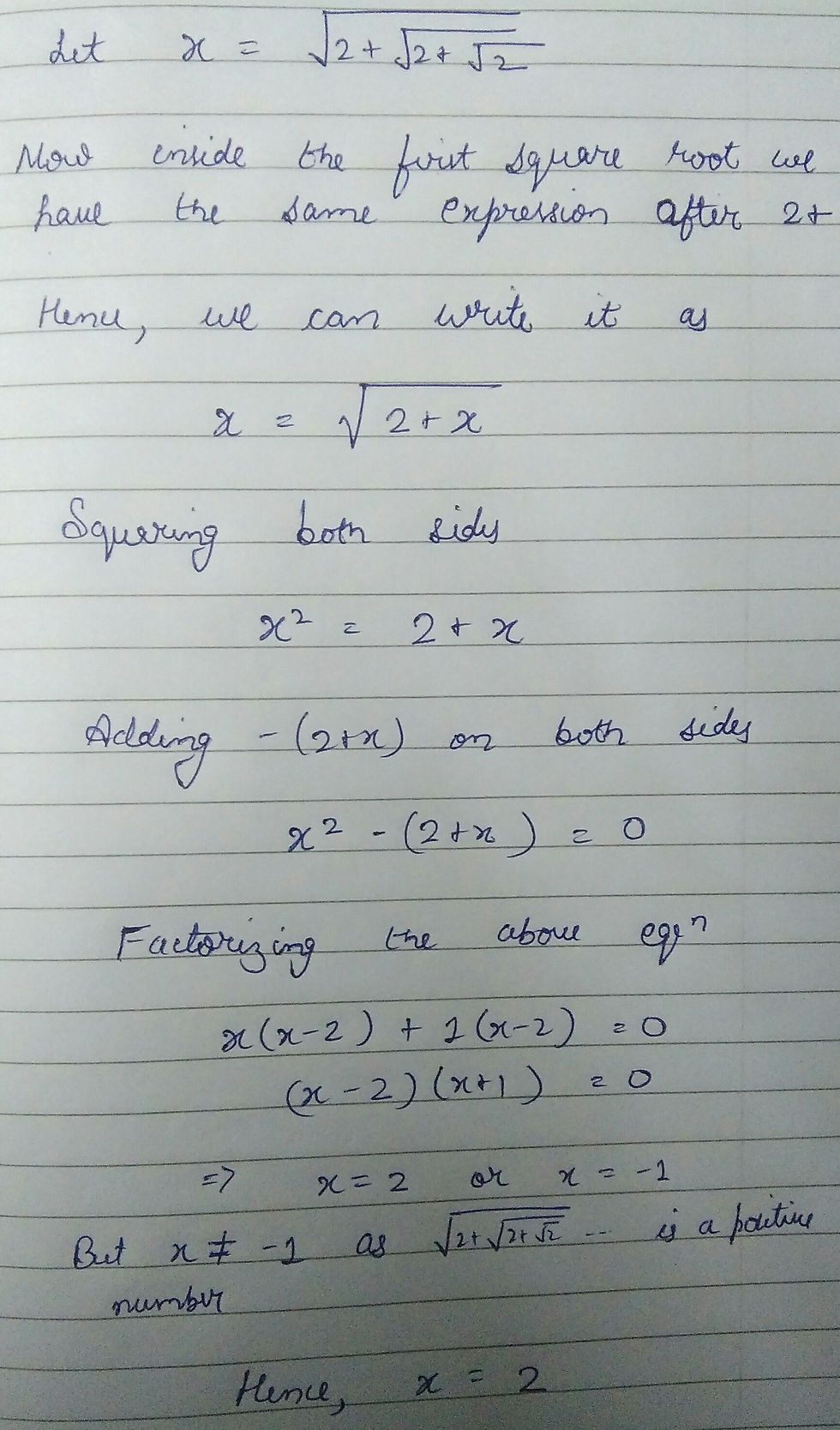
There are many more of them like these :

These were the mathematical proofs but how to analyse them so that we realize how things are working, here is how...

Now getting back to this original problem, Ramanujan's famous Radical

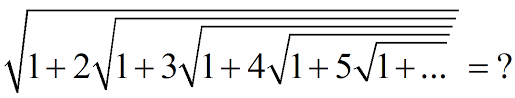
We cannot do this one by forming quadratic equation because it cannot be expressed in that kind of form here is how it is expressed:

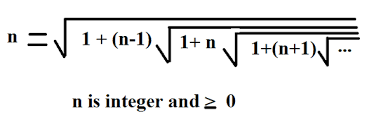
The formula proof for this was given by Ramanujan, can be found at the end of this article.

I am going to explain it to you guys how can we realize the same in a way I did it earlier.

That's it guys, hope you enjoyed the article and as always thanks for reading and have a good day.

Formal mathematical proof in Ramanujan's paper :