Inverse of a matrix using recursion.
- Jan 22, 2017
- 3 min read
In linear algebra, an nbyn square matrix A is called invertible (also non singular or nondegenerate) if there exists an n-by-n square matrix B such that

where In denotes the n-by-n identity matrix and the multiplication used is ordinary matrix multiplication. If this is the case, then the matrix B is uniquely determined by A and is called the inverse of A, denoted by A^(−1).
A square matrix that is not invertible is called singular or degenerate. A square matrix is singular if and only if its determinant is 0.
Matrix inversion is the process of finding the matrix B that satisfies the prior equation for a given invertible matrix A.
The method we are going to use is the relation of determinant with its Adjugate
The adjugate of a matrix can be used to find the inverse of A as follows:
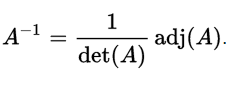
We have already seen how to calculate det(A), if you are directly reading this directly then I recommend to go and read how to calculate the determinant of the matrix.

Co-factor matrix ;
As we know that adjugate matrix is nothing but transpose of co-factor matrix and we can calculate co-factor matrix in the similar way we calculate the determinant.
Co-factor matrix is nothing but the determinant of the smaller matrix with respect to every element in the matrix, and take care of the sign (-1)^(i+j), where i,j represent the element of i(th) row and j(th) column.
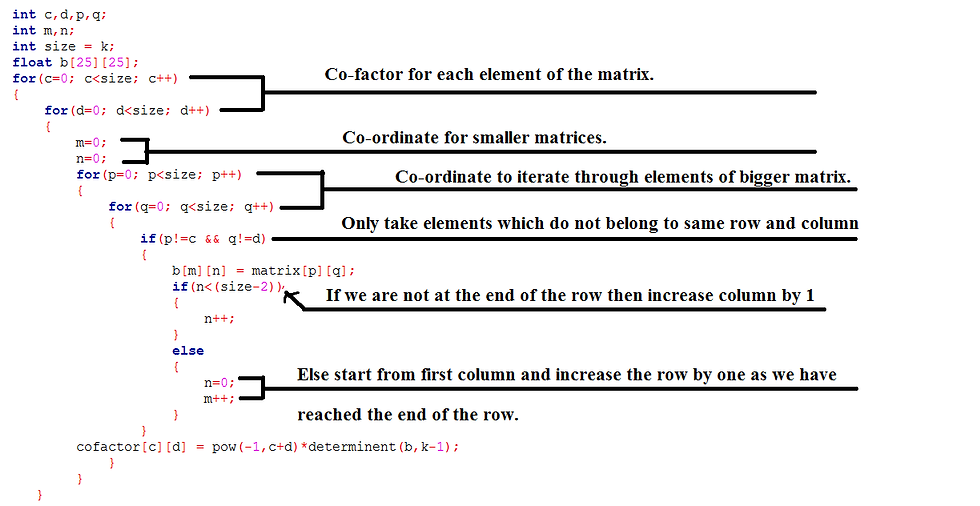
Now, that was similar to calculate the determinant the only change was that we have an extra for loop so that we can calculate determinant for all elements rather than calculating for the first row only.
Adjugate matrix :
In addition to this we need to take the transpose of the co-factor matrix in order to construct the adjugate matrix.
For this simply reverse the co-ordinate of each element of the co-factor matrix.

Inverse matrix :
Divide the whole matrix with determinant i.e iterate through element and divide each element by determinant.

That's it guys, we have successfully learnt how to find the inverse of a matrix, now you can code it yourself.
Happy coding!
Full C implementation/Code :
float determinent(float matrix[25][25], float size) { int c; float det=0,s=1; float b[25][25]; int i,j; int m,n; if(size == 1) { return (matrix[0][0]); }
else { det=0;
for(c=0; c<size; c++) { m=0; n=0; for(i=0; i<size; i++) { for(j=0; j<size; j++) { b[i][j] = 0; if(i!=0 && j!=c) { b[m][n] = matrix[i][j]; if(n<(size-2)) { n++; } else { n=0; m++; } } } }
det = det + s*(matrix[0][c]*determinent(b,size-1)); s = -1*s; } } return (det);
}
int main() { float k; printf("Enter the size n*n of the matrix "); scanf("%f",&k);
int i,j; float matrix[25][25]; for(i=0; i<k; i++) { for(j=0; j<k; j++) { printf("Enter the %d%d element of the matrix ",i,j); scanf("%f", &matrix[i][j]); } }
float result = determinent(matrix,k); printf("\nThe determinant of the matrix is %f",result);
float cofactor[25][25];
if(result == 0) printf("\nMatrix is singular, the inverse of the matrix does not exist\n");
else { int c,d,p,q; int m,n; int size = k; float b[25][25]; for(c=0; c<size; c++) { for(d=0; d<size; d++) { m=0; n=0; for(p=0; p<size; p++) { for(q=0; q<size; q++) { if(p!=c && q!=d) { b[m][n] = matrix[p][q]; if(n<(size-2)) { n++; } else { n=0; m++; } } cofactor[c][d] = pow(-1,c+d)*determinent(b,k-1); } } } } float Adjoint[25][25]; int s,t; for(s=0; s<k; s++) { printf("\n"); for(t=0; t<k; t++) { Adjoint[s][t] = cofactor[t][s]; } }
float Inverse[25][25]; int l,z; for(l=0; l<k; l++) { for(z=0; z<k; z++) { Inverse[l][z] = (Adjoint[l][z])/result; } }
int e,f; printf("The inverse of the matrix is"); for(e=0; e<k; e++) { printf("\n"); for(f=0; f<k; f++) { printf("%f ",Inverse[e][f]); } }
} printf("\n"); return 0;
}
Sample INPUT/OUTPUT :
2x2 matrix:
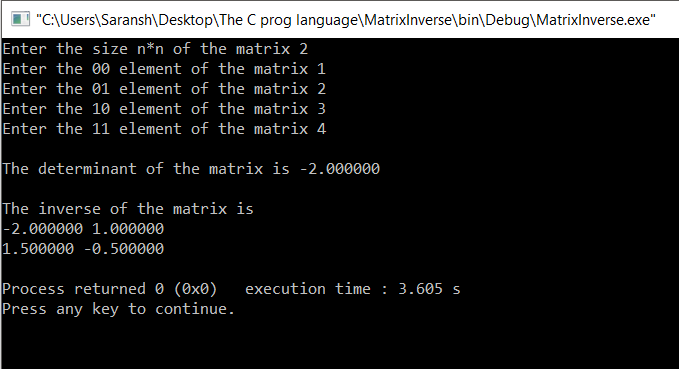
3x3 matrix:
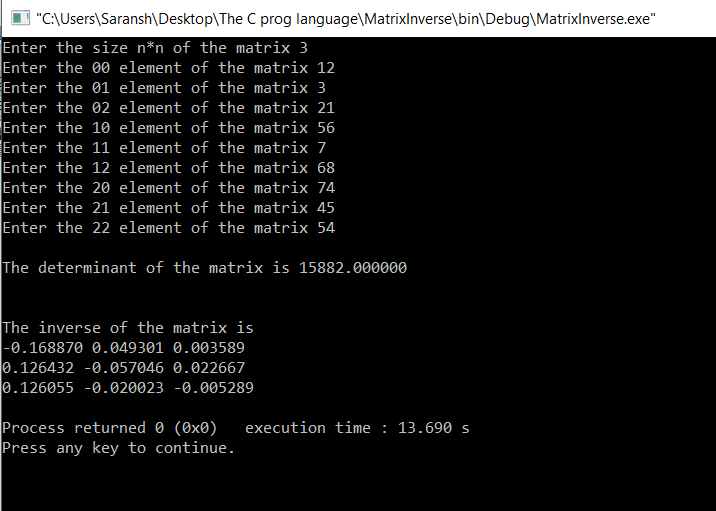
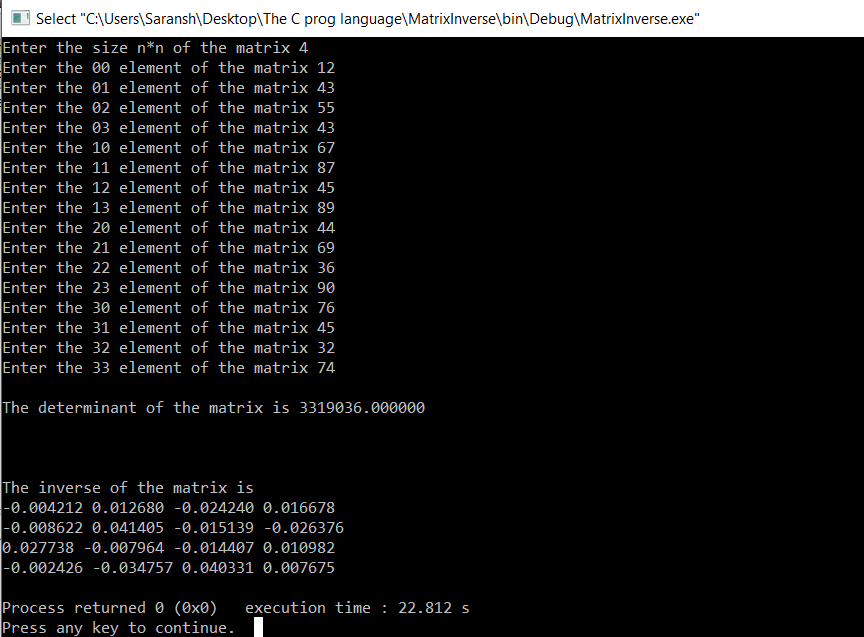
4x4 matrix:
Singular matrix :

You can verify these outputs, there is a really cool website for that :
Comments