Determinant of a matrix using recursion.
- Jan 22, 2017
- 3 min read
In linear algebra, the determinant is a useful value that can be computed from the elements of a square matrix. The determinant of a matrix A is denoted det(A), detA , or |A|. It can be viewed as the scaling factor of the transformation described by the matrix.
In the case of a 2 × 2 matrix, the specific formula for the determinant:
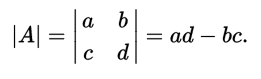
Similarly, suppose we have a 3 × 3 matrix A, and we want the specific formula for its determinant |A|:
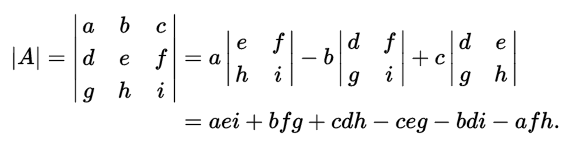
Each determinant of a 2 × 2 matrix in this equation is called a "minor" of the matrix A. The same sort of procedure can be used to find the determinant of a 4 × 4 matrix, the determinant of a 5 × 5 matrix, and so forth.
Now, we are going to find out the determinant of a matrix using recursion strategy.
Basically, we will exploit the property that determinant of 1x1 matrix is obviously the element present in the matrix. Using this we will try to see and understand how recursion can be used to get bigger and bigger cases using this base case.
Consider a 4x4 matrix, we can observe the recursive pattern while finding the determinant, the problem can be divided into sub problems of smaller smaller matrices and from these matrices the whole problem can traced as shown.

This tree is similar in programming what we call as recursive tree, the only difference is that while doing mathematics we can go in and order strictly from top to down while a recursive tree always follows top to down, left to right approach.
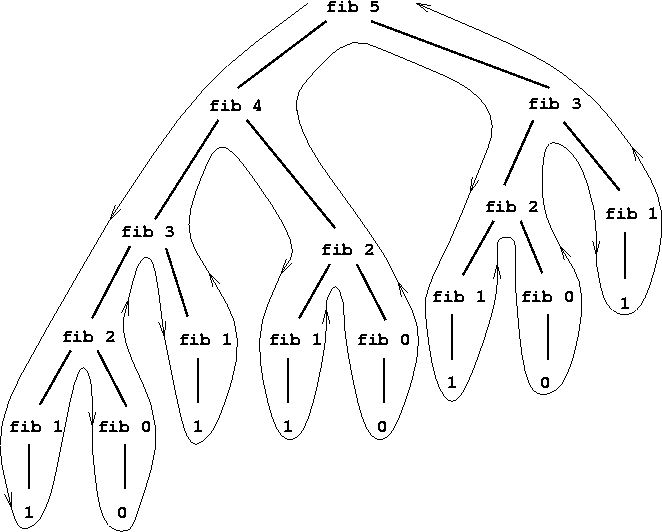
Now, to solve the problem we take care of the following things:
Note: We are choosing first row to calculate the determinant at each step. You can use any of them by modifying the code accordingly.
1) Base case:
When the size of matrix is 1x1 then we have the base case, we simply return value of the matrix in this case.

2) Recursive case
When the size of matrix is not one, the case is recursive and in that situation we need to take care of extra few things.

a) Sign (s)
Each time sign has been used, it must be reversed, initially we use s=1.

b) The next matrix (b)
While we are in first row calculating determinant, the next determinant will be calculated
leaving all other elements same but replacing the elements of the same row and column by 0.
This a bit tricky to understand at first but once you get the hang of it, it will be very simple.

That's all guys, we have successfully designed the logic for recursive calculation. A more advanced version of this problem can be to find the inverse of the matrix, I will attach a link for that but before going to that, i recommend you to take your time and clear your concept about recursion.
Note : This time, I have written the code in C language instead of C++ because C++ doesn't allow to pass 2D array directly into function arguments, though it can be done using pointers to array but my main motive in this problem was to introduce the concept of recursive functions.
Happy Coding!
Link :
Full C implementation/Code:
float determinent(float matrix[25][25], int size) { int c; float det=0,s=1; float b[25][25]; int i,j; int m,n; if(size == 1) { return (matrix[0][0]); }
else { det=0; for(c=0; c<size; c++) { m=0; n=0; for(i=0; i<size; i++) { for(j=0; j<size; j++) { b[i][j] = 0; if(i!=0 && j!=c) { b[m][n] = matrix[i][j]; if(n<(size-2)) { n++; } else { n=0; m++; } } } }
det = det + s*(matrix[0][c]*determinent(b,size-1)); s = -1*s; } } return (det);
}
int main() { int n; printf("Enter the size n*n of the matrix "); scanf("%d",&n);
int i,j; float matrix[25][25]; for(i=0; i<n; i++) { for(j=0; j<n; j++) { printf("Enter the %d%d element of the matrix ",i,j); scanf("%f", &matrix[i][j]); } }
float result = determinent(matrix,n); printf("The determinent of the matrix is %f",result);
}
Sample INPUT/OUTPUT :
2x2 matrix:
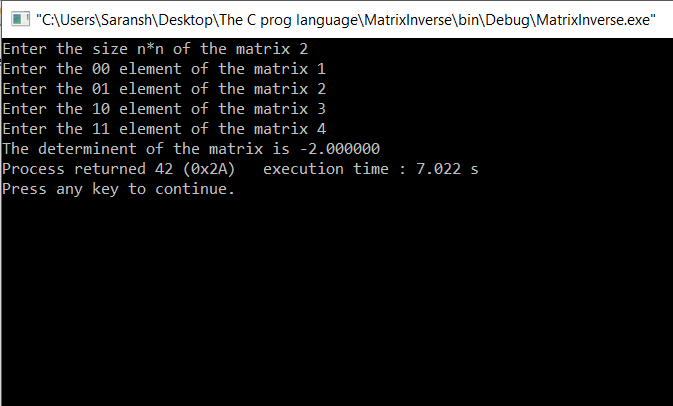
3x3 matrix:
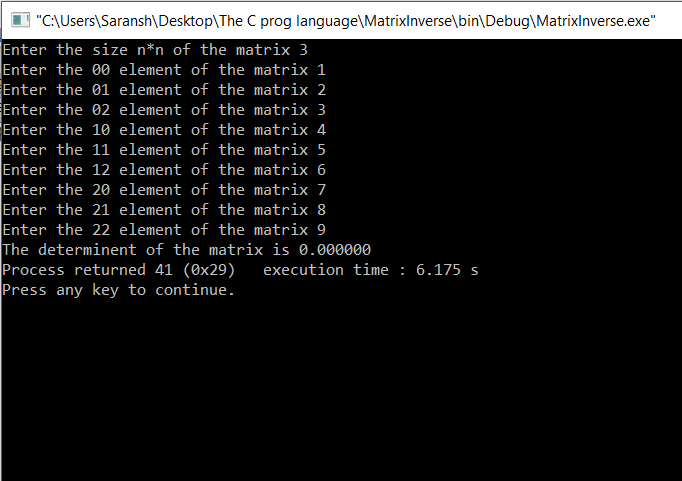
4x4 matrix:
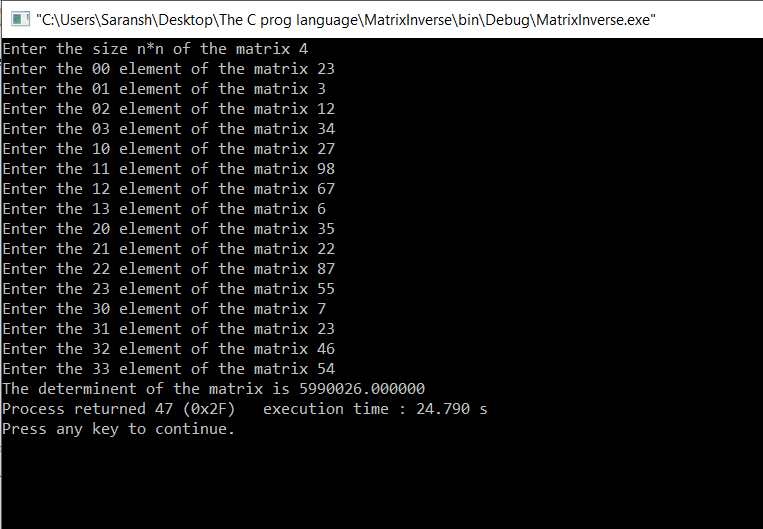
5x5 matrix:
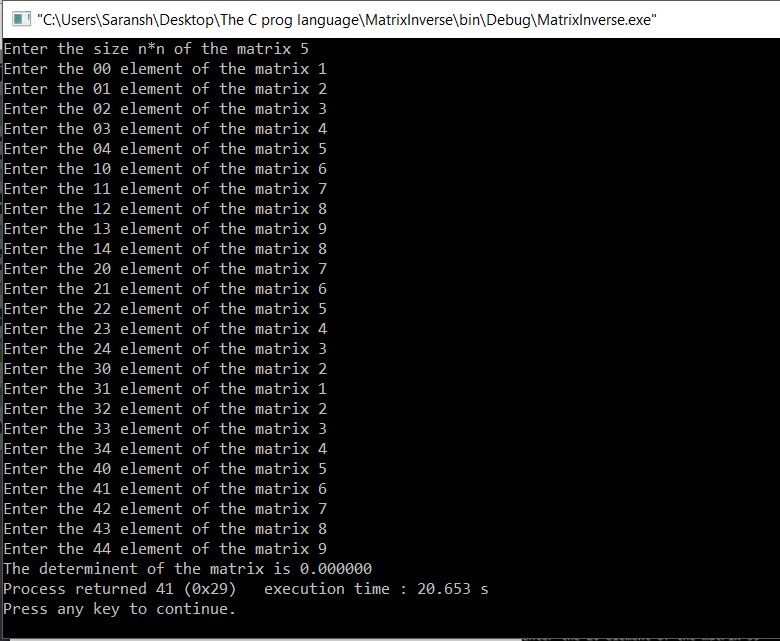
You can verify these results online there is a really cool website for that :
Comments