top of page

Zeno's Paradox

Zeno was a Greek philosopher who lived thousands of years ago and gave nine paradoxes, these paradoxes had gone through tremendous amount of research and there are people million times smarter than you and I who had battled with these paradoxes for thousands of years but somehow even today these paradoxes manage to baffle us in an amusing way, so today we are going to look at one of these paradoxes.

This paradox have baffled scientists for years and is quite simple to understand. Since the problem is thousands of years old, it talks about a character from Greek mythology, Achilles, the hero of the Trojan war, who once had a race with a tortoise, As the tortoise is slow while Achilles is fast and agile, in order to make the race a fair event, the tortoise is given a head start of say 'x' meters, now it doesn't matter how long the race is, to understand the paradox. Suppose, the race begin and Achilles run towards the tortoise, being fast he quickly reaches the point at which tortoise has started say 100 meters, now tortoise has moved on from that point say 20 meters and now Achilles has to cover the distance of 20 meters to catch up the tortoise but same thing happens again by the time Achilles will move to the point where the tortoise was previously the tortoise must have moved on and so in this way we can say that, Achilles will never be able to catch tortoise despite of having speed greater than tortoise,

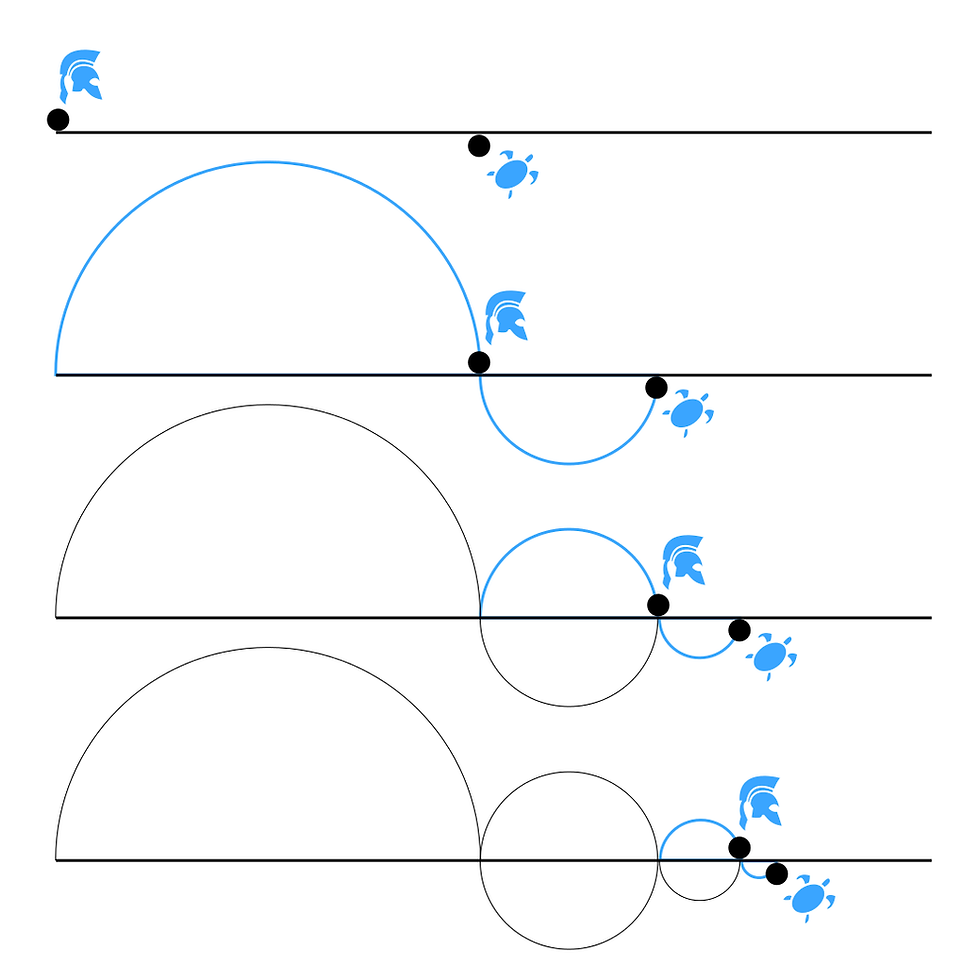
But if we think of this situation in real life, obviously Achilles will catch up, then why this thing mess up our basic intuition, I think that's because all these things are related to infinity, and yet we don't understand what infinity is completely, we cannot assign any value to it, we cannot think about its end because there is always more to it, we know it is large but how large?

The same goes with this problem, there are infinite amount of steps Achilles will take to complete the race but how can be an infinite process be completed.

One simple way to solve this paradox is relative velocity which my friend Mayank has suggested, he make some cool JAVA articles where you can learn JAVA starting from scratch you can check them out, the link is at the end of the article.

Mayank said that don't view the problem with respect to a third person perception, like you and I but from the perception of tortoise, what the tortoise will see if he had eyes on the back side, he will see Achilles approaching him closer and closer and finally crosses him, In physics the velocity which tortoise will see Achilles is approaching is Relative velocity which will be less than the velocity which you and I will observe, but then I countered Mayank's explaination by introducing another paradox, it goes this way, suppose tortoise is seeing Achilles approaching and the distance between them for instance be 2 meters, now imagine the tortoise cannot see backward and he wanted to cheat, he decided to interrupt Achilles as soon as he came parallel to him so he is equipped with a camera on his back which clicks the photograph of Achilles approaching him every time Achilles covers half the distance between Achilles and tortoise, in this way tortoise can monitor the progress of Achilles, now consider 0 delay between the image click and information sent to tortoise brain and unlimited supply of battery, Achilles will cover 1 meter in 1st photograph then 1/2 then 1/4 then 1/8 and so on, He has to cover the infinite amount of steps to reach the tortoise so the tortoise will keep on waiting for Achilles, but will Achilles ever reach the tortoise? How can infinite amount of work is done in finite amount of time? (See supertask) It is found that the sum 1+1/2+1/4.... approaches closer and closer to 2 and if one covers infinite amount of steps, then it is guaranteed that Achilles will cross the tortoise, here is the mathematics:

S = 1 + 1/2 + 1/4 + 1/8 + ......

S/2 = 1/2 + 1/4 + 1/8 + ......

_____________________________________

S-S/2 = 1

S/2 = 1

S = 2

So, we can see that Achilles has to cover infinite steps in order to reach the tortoise, the same logic can applied to time this at each step Achilles take half the time he has taken before, another way to understand this infinite series is that

We can write 2 as 1+ 1

We can write 1 as 1/2 + 1/2

We can write 1/2 as 1/4 + 1/4

Again 1/4 can be written as 1/8 + 1/8

and the series goes on and on, this is how Ramanujan explained this expression equal to 3.

(For proof click here).

But, let's focus on the paradox for now. We have seen everytime we try to solve the problem this infinity pops up and that's why we need to solve this infinity problem.

Infinity relationship with finiteness can be seen from very simple examples, consider a right angled triangle with base and height being equal to one, now from pythagoras theorem, we know that hypoteneus will be equal to square root of 2 which is irrational, means it has no ends to its decimal digits but there is nothing that can stop me drawing this length, how is that possible?

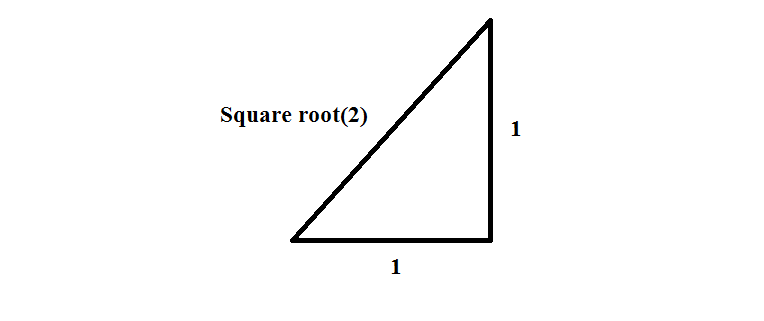
In order to solve this paradox and many related problems the way I explained this, I would like to introduce a term called plank's length, which is defined in physics as the smallest measurement of length with any meaning and roughly equal to 1.6 x 10^(-35) m or about 10^(-20) times the size of a proton Anything shorter than that is meaningless and that is what I think is key to solve the problem, No matter what happens Achilles has to cover this much amount of distance in one go, he cannot half the distance or divide this distance in any amount and this is the ultimate limit just like other limits, i.e speed of light, absolute zero etc. Similarly if we try to make a line segment of length of square root of 2 we will able to do it upto the precision of this range, then what will happen I don't know.

This fact is absolutely amazing, this topic brings mathematics and physics together, this is absolute beauty, the planck's length. A lot of research is still needed before we finally reach the conclusion but that is how I explain things.

Don't worry if it baffles with your mind, it is a paradox doing its job.

Thanks for reading folks, have a nice day!


bottom of page