Prime factorization
- Jan 19, 2017
- 2 min read
Problem credits : Codechef
Section : Challenge

The Fundamental theorem of arithmetic (also called the unique factorization theorem) is a theorem of number theory. The theorem says that every positive integer greater than 1 can be written as a product of prime numbers (or the integer is itself a prime number). The theorem also says that there is only one way to write the number. If two people found two different ways to write the number, the only thing that can be different is the order in which the primes are written. For example, we can write:

Note : These examples will be tested in the Sample INPUT/OUTPUT section below.
The way I solved this problem that I divided the problem in several steps then defined some functions for some steps and rest of the task is done main function.
Step by step approach :
1) Calculate the factors normally and store them in one array;
LOGIC : Divide the number starting from 2 to n/2 and if remainder is zero then store it in the array.
Why n/2 : Because after n/2 number there will not exist any factor except the number itself
ex : 25/2 = 12, and we have no factor greater than 12 for 25.

2) Now check the factors, if they are prime then store them in another array;
LOGIC : To check whether a factor is prime or not just follow step 1 logic and break the loop as soon as you get a factor.

3) Now we have factors, prime factors but we don't know how many occurrence of a prime factor is there i.e prime factors of 20 are 2 and 5 but 2 occurs 2 times in factorization.
LOGIC : Define a function which calculates no. of primes, the way it is done is for example check how many times 2 divides 24 and increment some counter and store that counter value.

4) Now we just need to display the prime factor as many times it occurs in the final OUTPUT

The problem can also be found on Codechef, challenge section, they presented the problem in this way
You are given an integer N, you need to find M positive integers A1, A2, A3, ..., AM, so that A1*A2*A3*...*AMwould be equal to N. You should maximize the number M.
Obviously, maximizing M means expressing N as product of smallest number possible i.e prime numbers.
Link : https://www.codechef.com/problems/FACTORIZ
Full C++ Implementation/Code:
bool numberIsprime(int k) { int j; int fact = 0; for(j=2; j<=k/2; j++) { if(k%j == 0) { fact++; break; } else continue; } if(fact == 0) return true; else return false; }
int primeCount(int l, int n) { int w=0; while(n%l == 0) { w++; n = n/l; } return w; }
int main() { int n; cout<<"Enter the number "; cin>>n; int factorArray[n];
int i; int p=0; for(i=2; i<=n/2; i++) { if(n%i == 0) { factorArray[p] = i; p++;
}
}
int r; int primefactorArray[n]; int q=0; for(r=0; r<p; r++) { if(numberIsprime(factorArray[r])) { primefactorArray[q] = factorArray[r]; q++; } }
int howmanyPrimes[n]; int t; for(t=0; t<q; t++) { howmanyPrimes[t] = primeCount(primefactorArray[t],n);
}
int k,f; cout<<n<<" = "; for(k=0; k<q; k++) { for(f=0; f<howmanyPrimes[k]; f++) { cout<<primefactorArray[k]<<"."; } } cout<<endl; return 0;
}
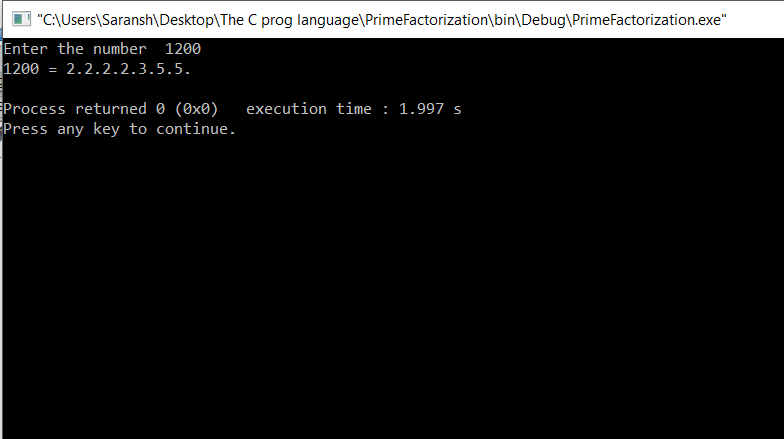
Sample INPUT/OUTPUT:
6936 :

1200 :
Comments