Puppy and Triangles
- Jan 17, 2017
- 4 min read
Puppy Tuzik has recently found two triangles and a quadrilateral cut out from a large sheet of paper. Being a curious puppy, Tuzik started thinking of a game with these three geometric figures. All of a sudden, a thrilling idea crossed his mind! He wonders whether it's possible to combine these triangles by moving, flipping and/or rotating them, and cover exactly the quadrilateral with no overlap between the two triangles. Giving the coordinates of the triangles and the quadrilateral, your task is to answer the question: whether it's possible to combine the triangles to cover exactly the given quadrilateral?
Input format: Three points for 2 triangles each of the from (x,y)
Four points for the quadrilateral each of the form (x,y)
Output format: Yes or No
The problem will be more clear from the following examples
Note : These examples will be verified by program in the end of this article.
Fitting case:
Coordinates for the 1st triangle: (0 0) (1 0) (1 1)
Coordinates for the 2nd triangle: (3 3) (2 2) (3 2)
Coordinates for the quadrilateral: (5 5) (5 4) (4 4) (4 5)
Graphically, the distribution of points and line segments will look like this:
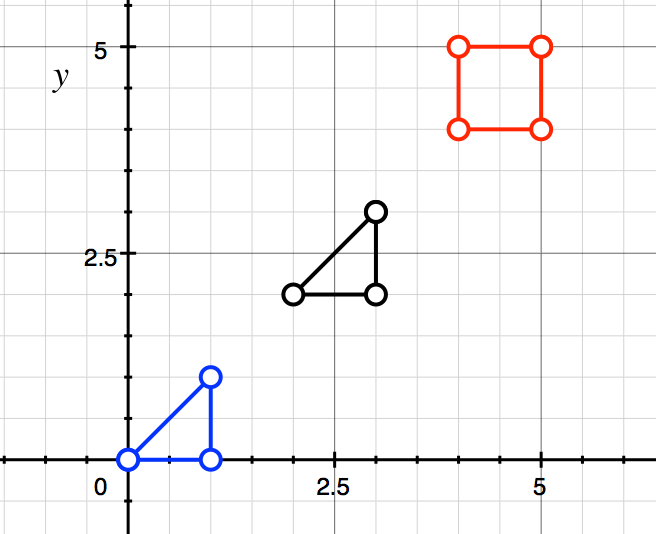
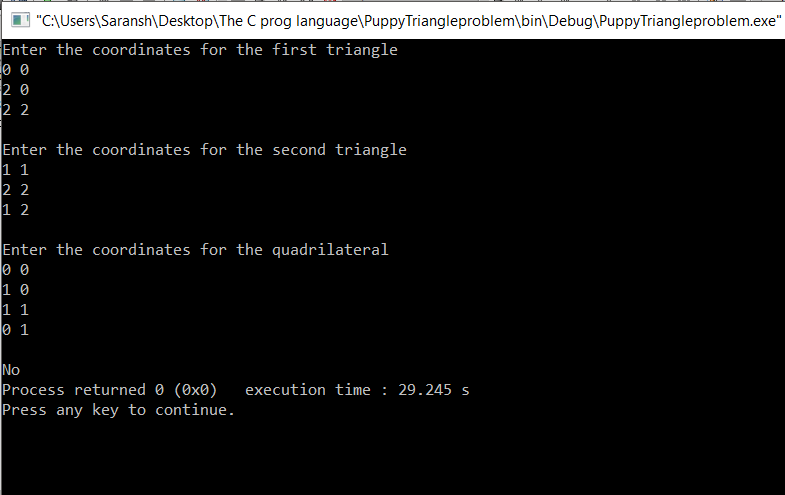
Non-fitting case:
Coordinates for the 1st triangle: (0 0) (2 2) (2 0)
Coordinates for the 2nd triangle: (1 1) (1 2) (2 2)
Coordinates for the quadrilateral: (0 0) (0 1) (1 1) (1 0)
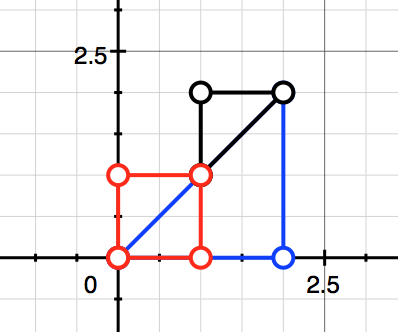
LOGIC:
There is only one way in which a quadrilateral can be cut into 2 pieces of triangles, along the diagonal. If we try in some other way we will either get 2 quadrilateral or 1 polygon and one triangle, this will be clear from the following figure.
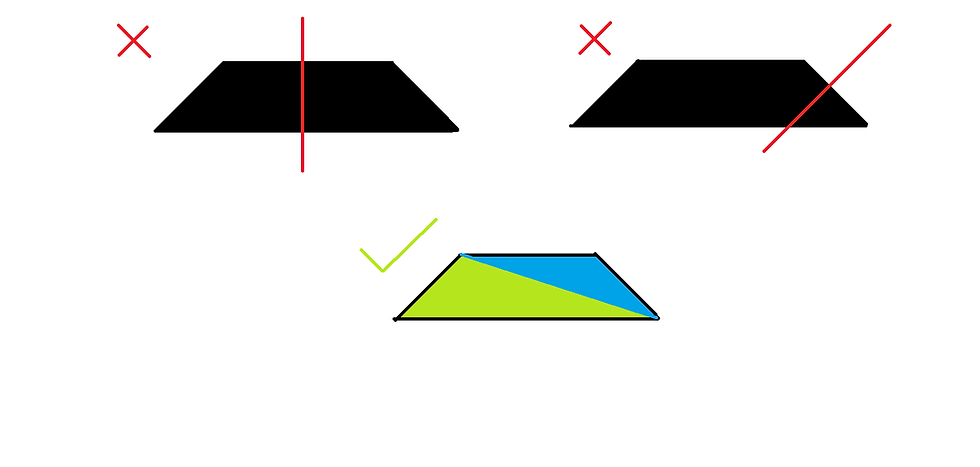
So there are two possible diagonals which must have to be equal to one of the sides of both triangles:
Suppose, diagonal d1 is equal to any one of the sides of triangle 1 and also equal to any one of the side of triangle 2,
Now the other two sides of quadrilateral must also be equal to other two sides of the triangle
And same goes for diagonal d2.
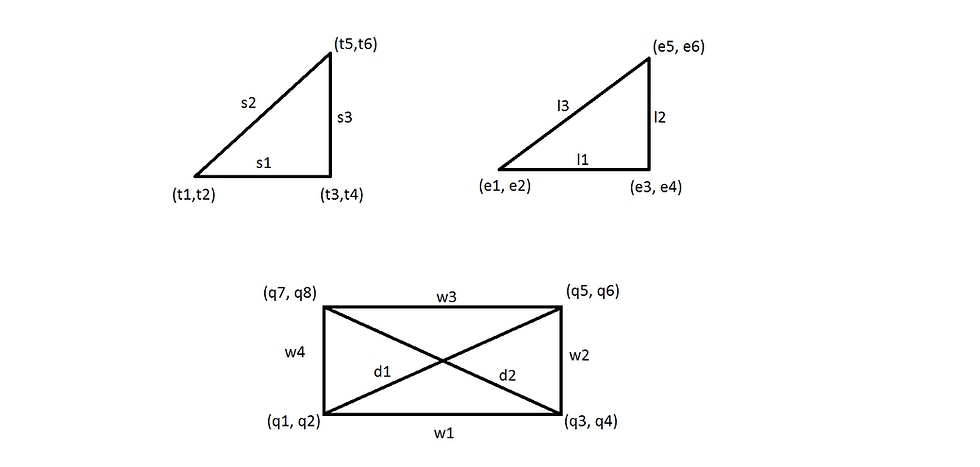
We are going to use distance formula to get the distance between two points (x1, y1) and (x2, y2).
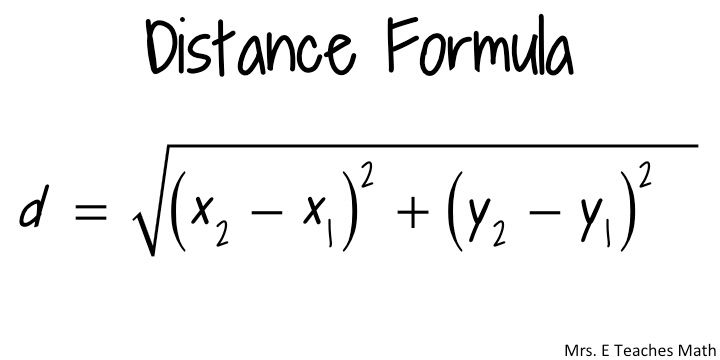
Now, we have all the information to crack the problem, let's dive into coding
Calculating length of sides of triangles and sides and diagonals of quadrilateral.

Here, pow(x,y) means x raised to the power y and sqrt(z) means square root of z.
Defining boolean variables to compare the sides and diagonals of quadrilateral with the sides of the triangles.

Now first check if there exist a diagonal which has common length with both of the triangle

Now if diagonal d1 matches then we have two possibilities triangle 1 in upper compartment and triangle 2 in lower compartment and vice-versa.
For upper compartment compare w3, w4 and d1 with sides of triangles
For lower compartment compare w1, w2 and d1 with sides of triangles
Same goes for d2.
For d1:

Else for d2:

That's it guys, we just have solved a problem from the hard section of codechef.com
Full C++ implementation/CODE:
using namespace std;
int main() { int t1,t2,t3,t4,t5,t6; //Coordinates for the first triangle; int e1,e2,e3,e4,e5,e6; //Coordinates for the second triangle; int q1,q2,q3,q4,q5,q6,q7,q8; //Coordinates for the quadrilateral
cout<<"Enter the coordinates for the first triangle"<<endl; cin>>t1>>t2; cin>>t3>>t4; cin>>t5>>t6; cout<<endl;
cout<<"Enter the coordinates for the second triangle"<<endl; cin>>e1>>e2; cin>>e3>>e4; cin>>e5>>e6; cout<<endl;
cout<<"Enter the coordinates for the quadrilateral"<<endl; cin>>q1>>q2; cin>>q3>>q4; cin>>q5>>q6; cin>>q7>>q8; cout<<endl;
float s1,s2,s3; // Side length of the first triangle float l1,l2,l3; // Side length of the second triangle float w1,w2,w3,w4,d1,d2; // Side and diagonal lengths of the quadrilateral
//Lengths of sides of first triangle s1 = sqrt(pow((t1-t3),2)+pow((t2-t4),2)); s2 = sqrt(pow((t1-t5),2)+pow((t2-t6),2)); s3 = sqrt(pow((t5-t3),2)+pow((t6-t4),2));
//Lengths of sides of second triangle l1 = sqrt(pow((e1-e3),2)+pow((e2-e4),2)); l2 = sqrt(pow((e1-e5),2)+pow((e2-e6),2)); l3 = sqrt(pow((e5-e3),2)+pow((e6-e4),2));
//Lengths of sides and diagonals of second triangle w1 = sqrt(pow((q1-q3),2)+pow((q2-q4),2)); d1 = sqrt(pow((q1-q5),2)+pow((q2-q6),2)); w2 = sqrt(pow((q5-q3),2)+pow((q6-q4),2)); w3 = sqrt(pow((q5-q7),2)+pow((q6-q8),2)); d2 = sqrt(pow((q7-q3),2)+pow((q8-q4),2)); w4 = sqrt(pow((q7-q1),2)+pow((q8-q2),2));
bool a = d1==s1, b = d1==s2, c = d1==s3, d = d1==l1, e = d1==l2, f = d1==l3; bool g = d2==s1, h = d2==s2, i = d2==s3, j = d2==l1, k = d2==l2, l = d2==l3; bool m = w1==s1, n = w1==s2, o = w1==s3, p = w1==l1, q = w1==l2, r = w1==l3; bool s = w2==s1, t = w2==s2, u = w2==s3, v = w2==l1, w = w2==l2, x = w2==l3; bool y = w3==s1, z = w3==s2, a1 = w3==s3, b1 = w3==l1, c1 = w3==l2, d11 = w3==l3; bool e11 = w4==s1, f1 = w4==s2, g1 = w4==s3, h1 = w4==l1, i1 = w4==l2, j1 = w4==l3;
if(((a || b || c) && (d || e || f)) || ((g || h || i) && (j || k || l))) // Two triangles have one side in common with one of the diagonal { if((a || b || c) && (d || e || f)) { if((m || n || o) && (s || t || u) && (b1 || c1 || d11) && (h1 || i1 || j1)) { cout<<"YES"; }
else if((y || z || a1) && (e11 || f1 || g1 ) && (p || q || r) && (v || w || x)) { cout<<"YES"; }
else { cout<<"No"; } }
else { if((w1 == s1||s2||s3) && (w4 == s1||s2||s3) && (w2 == l1||l2||l3) && (w3 == l1||l2||l3)) { cout<<"YES"; } else if((w2 == s1||s2||s3) && (w3 == s1||s2||s3) && (w1 == l1||l2||l3) && (w4==l1||l2||l3)) { cout<<"YES"; } else { cout<<"No"; } } } else { cout<<"No"; }
}
Sample INPUT/OUTPUT:
Fitting case:

Non-fitting case:
Comments