Maximum matrix duplet
- Jan 15, 2017
- 3 min read
Problem statement :
You are given a square matrix n*n and you have to find the maximum duplet, where a duplet is defined as a set of two elements from a matrix occurring side by side or diagonally and when the elements are added, the duplet having the maximum sum is the maximum duplet. So the problem is simple, find the maximum duplet in the n*n matrix.
We will understand this with the help of some examples :
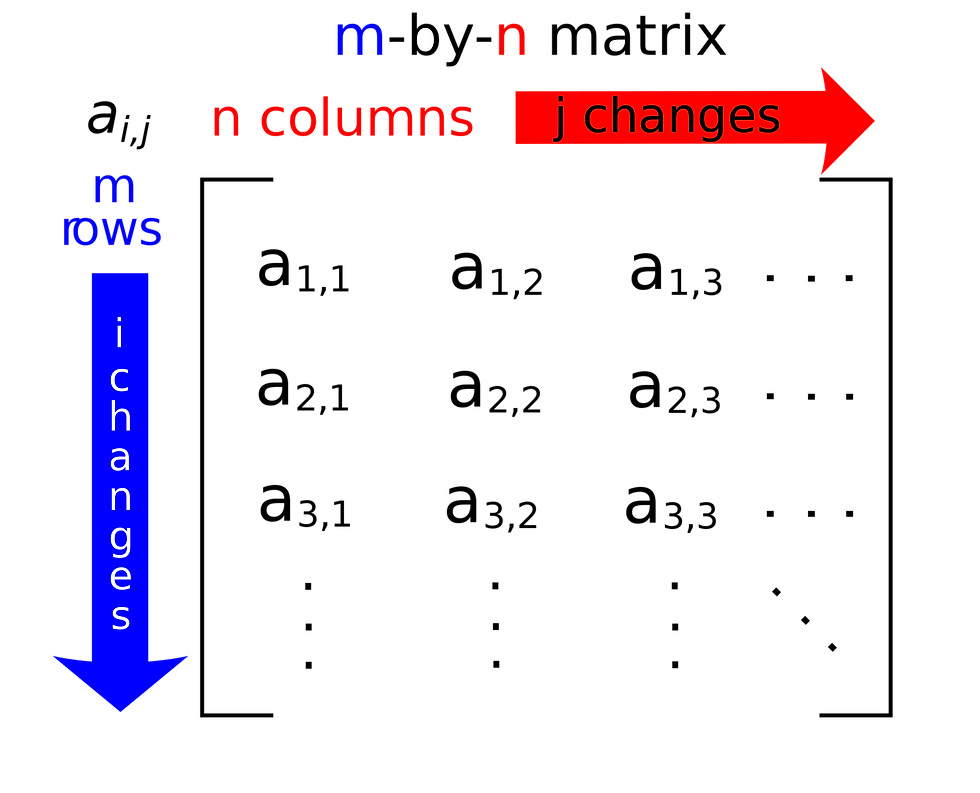

There could be many ways to solve this problem like divide the problem into sub problems
and then finding the optimal solution. i.e divide the bigger matrix into smaller smaller matrices and then find the solution.
Note : The optimal solution of the problem will depend upon the optimal solution of the sub-problems.
But, the way I solved is very easy and understandable. My basic strategy is to pick up elements from the matrix and compare them in the following fashion :


Let's call it as 3-way comparison.
Now, there are two things to note here
1) I have to exclude the elements from the last row as well as last column as for last column elements there do not exist any horizontal and diagonal element to compare, similarly for last row elements there do not exist any vertical and diagonal elements.

2) Though this seems to be correct but there is a flaw in this, we are ignoring the left diagonal elements from comparison.

Let get into a little bit of coding.
The way i implemented the code is that I am searching for maximum duplet according to individual element then storing it in the array, then I am storing the last row and column elements combos in the same array and then left diagonal elements in the same array.
So, we need a total of 4*n*(n-1) elements for the array, here is how.
a) 3 way comparison gives us a total of 2*(n-1)*(n-1) elements.
b) Left over row and column comparison gives us a total of 2*(n-1) elements.
c) Left diagonal comparisons gives us 2*n*(n-1).
If we sum up above comparisons we get 4*n*(n-1) elements.
3-way comparison
Left over row and column comparison

Left diagonal elements

As the elements occur in pairs in final array all we have to do is to find the sum of two successive elements and get the maximum duplet out of them.

C++ implemented full code :
int maximum(int a, int b, int c) { if(a>=b && b>c) return a; else if(b>=c) return b; else return c; }
int main() { cout<<"Enter the size of matrix\n"; int n; cin>>n; cout<<endl; int matrix[n][n]; int p,q; for(p=0; p<n; p++) { for(q=0; q<n; q++) { cout<<"Enter the value "<<p<<q<<" "; cin>>matrix[p][q]; } } cout<<endl;
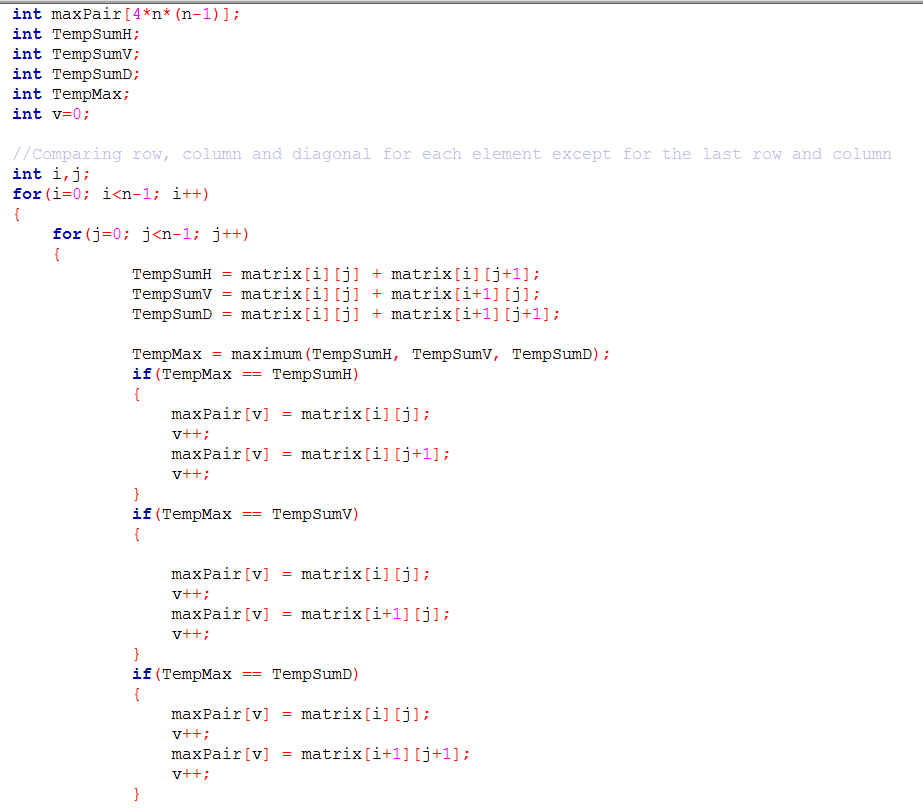
int maxPair[4*n*(n-1)]; int TempSumH; int TempSumV; int TempSumD; int TempMax; int v=0;
//Comparing row, column and diagonal for each element except for the last row and column int i,j; for(i=0; i<n-1; i++) { for(j=0; j<n-1; j++) { TempSumH = matrix[i][j] + matrix[i][j+1]; TempSumV = matrix[i][j] + matrix[i+1][j]; TempSumD = matrix[i][j] + matrix[i+1][j+1];
TempMax = maximum(TempSumH, TempSumV, TempSumD); if(TempMax == TempSumH) { maxPair[v] = matrix[i][j]; v++; maxPair[v] = matrix[i][j+1]; v++; } if(TempMax == TempSumV) {
maxPair[v] = matrix[i][j]; v++; maxPair[v] = matrix[i+1][j]; v++; } if(TempMax == TempSumD) { maxPair[v] = matrix[i][j]; v++; maxPair[v] = matrix[i+1][j+1]; v++; }
}
}
int h; for(h=0; h<n-1; h++)//Getting the last row { maxPair[v] = matrix[n-1][h]; v++; maxPair[v] = matrix[n-1][h+1]; v++;
}
int x; int SumV = 0; //Getting the last column for(x=0; x<n-1; x++) { maxPair[v] = matrix[x][n-1]; v++; maxPair[v] = matrix[x+1][n-1]; v++;
}
int ld1,ld2; for(ld1=0; ld1<n-1; ld1++) { for(ld2=1; ld2<n; ld2++) {
maxPair[v] = matrix[ld1][ld2]; v++; maxPair[v] = matrix[ld1+1][ld2-1]; v++;
} }
int g; int MaxSum = 0; int Pair[2]; for(g=0; g<4*n*(n-1); g++) { if(MaxSum <= maxPair[g] + maxPair[g+1]) { MaxSum = maxPair[g] + maxPair[g+1]; Pair[0] = maxPair[g]; Pair[1] = maxPair[g+1]; } g++; } cout<<"Maximum sum is "<<Pair[0]+Pair[1]<<endl; cout<<"Max Sum Combination is "<<Pair[0]; cout<<","<<Pair[1]<<endl;
}
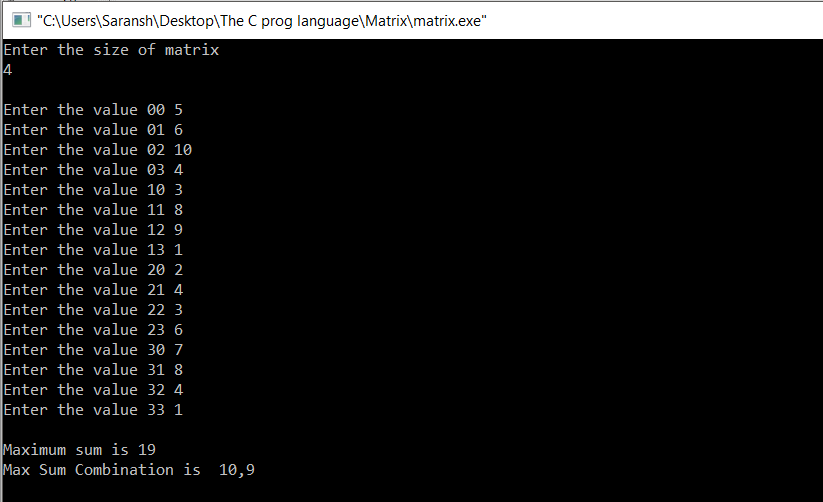
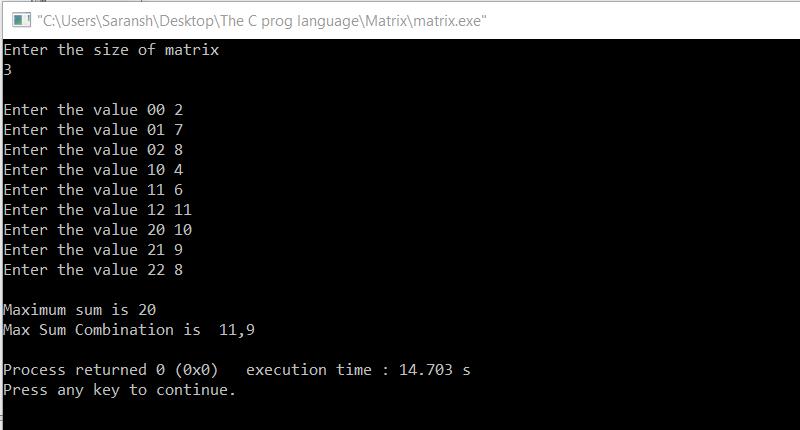
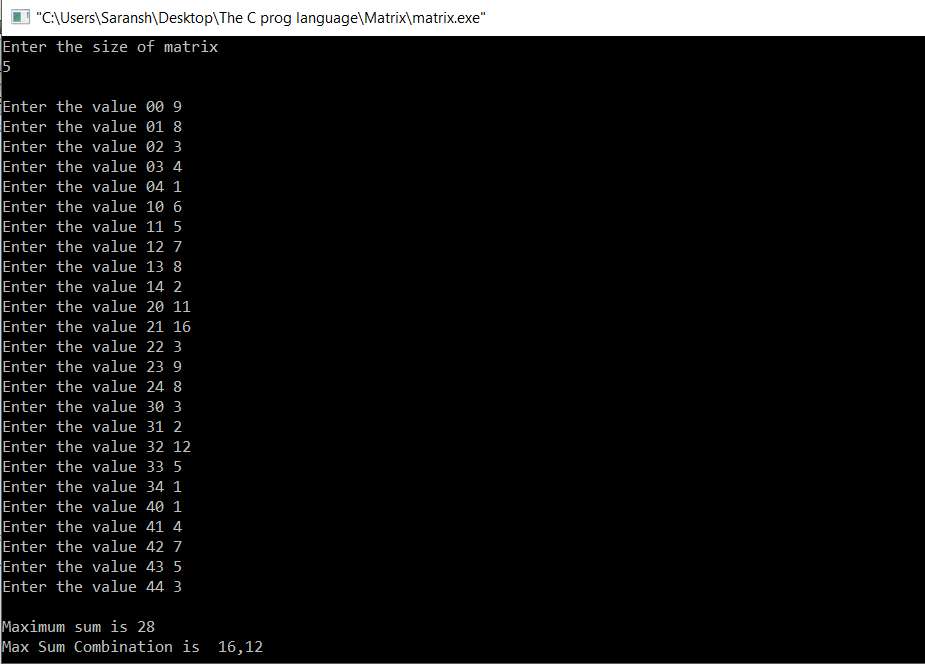
Sample INPUT/OUTPUT :
We can verify the duplets of the matrices that I mentioned above.

Comments